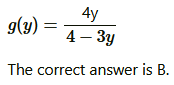NCERT SOLUTIONS FOR CLASS 12 MATHS CHAPTER 1-RELATIONS AND FUNCTIONS EXERCISE 1.3
NCERT solutions for class 12 maths Chapter 1 Relation and Functions are prepared by the academic team of Nashad. we have prepared NCERT Solutions for all exercises of chapter 1. Given below is a step-by-step solution to all questions given in the NCERT textbook for Chapter 1 Relations and Functions.
Solve The Following Questions.
Question1. Let f: {1, 3, 4} → {1, 2, 5} and g: {1, 2, 5} → {1, 3} be given by f = {(1, 2), (3, 5), (4, 1)} and g = {(1, 3), (2, 3), (5, 1)}. Write down gof.
Solution :
Question2. Let f,g, and h be functions from R to R. Show that:
(f + g)oh = foh + goh
(f.g)oh = (foh). (goh)
Solution :

Question3. Find gof and fog, if:
(i) f(x) = |x| and g(x) = |5x – 2|
(ii) f(x) = 8x3 and g(x) = x1/3
Solution :
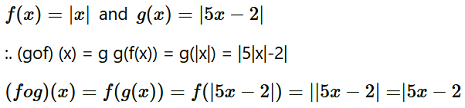
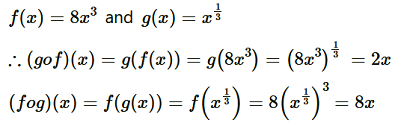
Question4. If show that fof (x) = x for all x ≠ 2/3 What is the inverse of f
Solution :
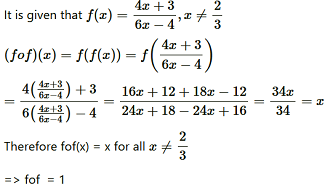
Hence, the given function f is invertible and the inverse of f is itself.
Question5. State with reason whether the following functions have an inverse
(i) f: {1, 2, 3, 4} → {10} with f = {(1, 10), (2, 10), (3, 10), (4, 10)}
(ii) g: {5, 6, 7, 8} → {1, 2, 3, 4} with g = {(5, 4), (6, 3), (7, 4), (8, 2)}
(iii) h: {2, 3, 4, 5} → {7, 9, 11, 13} with h = {(2, 7), (3, 9), (4, 11), (5, 13)}
Solution :
(i) f: {1, 2, 3, 4} → {10}defined as:
f = {(1, 10), (2, 10), (3, 10), (4, 10)}
From the given definition of f, we can see that f is a many one function as: f(1) = f(2) = f(3) = f(4) = 10
∴f is not one-one.
Hence, function f does not have an inverse.
(ii) g: {5, 6, 7, 8} → {1, 2, 3, 4} defined as:
g = {(5, 4), (6, 3), (7, 4), (8, 2)}
From the given definition of g, it is seen that g is a many one functions as g(5) = g(7) = 4.
∴g is not one-one,
Hence, function g does not have an inverse.
(iii) h: {2, 3, 4, 5} → {7, 9, 11, 13} defined as:
h = {(2, 7), (3, 9), (4, 11), (5, 13)}
It is seen that all distinct elements of the set {2, 3, 4, 5} have distinct images under h.
∴Function h is one-one.
Also, h is onto since for every element y of the set {7, 9, 11, 13}, there exists an element x in the set {2, 3, 4, 5}such that h(x) = y.
Thus, h is a one-one and onto function. Hence, h has an inverse.
Question6. Show that f: [-1,1] → R given by f(x) = x/x+2 is one-one. Find the inverse of the function f: [-1,1] → Range f
Solution :

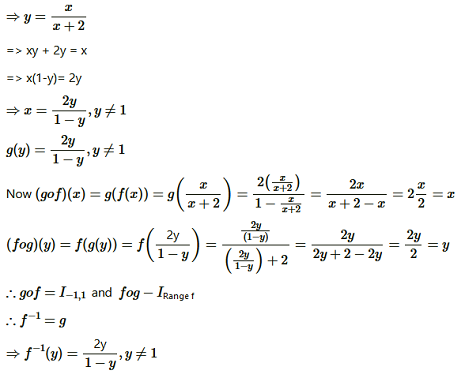
Question7. Consider f : R→ R given by f(x) = 4x + 3 Show that f is invertible. Find the inverse of f.
Solution :
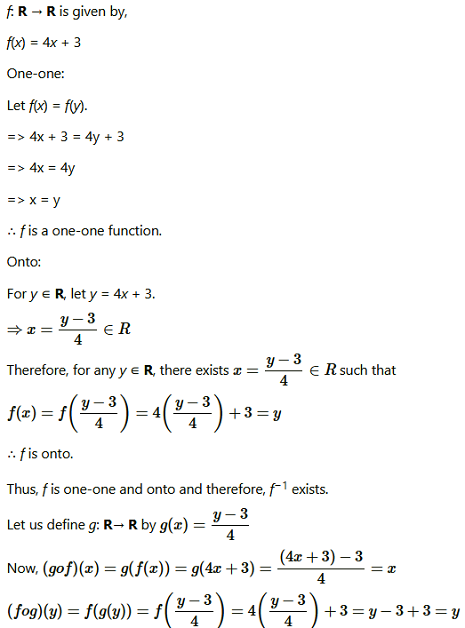
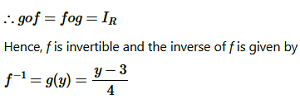
Question8. Consider f: R+ → [4, ∞) given by f(x) = x2 + 4 Show that f is invertible with the inverse f−1 of f given by f−1(y) = √y – 4 where R+ is the set of all non-negative real numbers.
Solution :

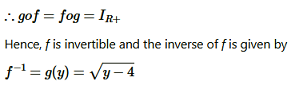
Question9. Consider f: R+ → [−5, ∞) given by f(x) = 9x2 + 6x − 5. Show that f is invertible with
Solution :


Question10. Let f: X → Y be an invertible function. Show that f has unique inverse.
(Hint: suppose g1 and g2 are two inverses of f. Then for all y ∈ Y, fog1(y) = IY(y) = fog2(y). Use one-one ness of f).
Solution :

Question11. Consider f: {1, 2, 3} → {a, b, c} given by f(1) = a, f(2) = b and f(3) = c. Find f−1 and show that (f−1)−1 = f.
Solution :

Question12. Let f: X → Y be an invertible function. Show that the inverse of f−1 is f, i.e., (f−1)−1 = f.
Solution :
Let f: X → Y be an invertible function.
Then, there exists a function g: Y → X such that gof = IXand fog = IY.
Here, f−1 = g.
Now, gof = IX and fog = IY
⇒ f−1of = IX and fof−1= IY
Hence, f−1: Y → X is invertible and f is the inverse of f−1
i.e., (f−1)−1 = f.
Question13. 
(A) 1/x3
(B) x3
(C) x
(D) (3 − x3)
Solution :
Question14.

Solution :