NCERT solutions for class 12 maths Chapter 1 Relations and Functions is prepared by the academic team of Nashad. We have prepared NCERT Solutions for all exercise of chapter 1. Given below is a step-by-step solution to all questions given in NCERT textbook for Chapter 1 Relations and Functions.
NCERT Solutions for Class 12 Maths Miscellaneous Exercise
Solve The Following Questions.
Question1. Let f: R → R be defined as f(x) = 10x + 7. Find the function g: R → R such that g o f = f o g = 1R.
Solution :


Question2. Let f: W → W be defined as f(n) = n − 1, if it is odd and f(n) = n + 1, if n is even. Show that f is invertible. Find the inverse of f. Here, W is the set of all whole numbers.
Solution :


Question3. If f: R → R is defined by f(x) = x2 − 3x + 2, find f(f(x)).
Solution :

Question4. Show that function f: R → {x ∈ R: −1 < x < 1} defined by f(x) = x/1+|x| x ∈R is one-one and onto function.
Solution :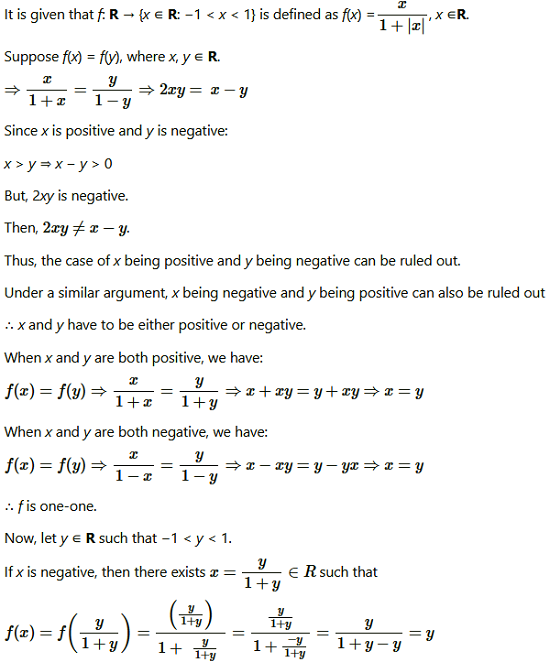

Question5. Show that the function f: R → R given by f(x) = x3 is injective.
Ans f: R → R is given as f(x) = x3.
Suppose f(x) = f(y), where x, y ∈ R.
⇒ x3 = y3 … (1)
Now, we need to show that x = y.
Suppose x ≠ y, their cubes will also not be equal.
⇒ x3 ≠ y3
However, this will be a contradiction to (1).
∴ x = y
Hence, f is injective.
Question6. Give examples of two functions f: N → Z and g: Z → Z such that g o f is injective but g is not injective.
(Hint: Consider f(x) = x and g(x) = |x| )
Solution :
Question 7. Given examples of two functions f: N → N and g: N → N such that gof is onto but f is not onto.
(Hint: Consider f(x) = x + 1 and )
Solution :

Question8. Given a non-empty set X, consider P(X) which is the set of all subsets of X.
Define the relation R in P(X) as follows: For subsets A, and B in P(X), ARB if and only if A ⊂ B. Is R an equivalence relation on P(X)? Justify your answer:
Solution :
Since every set is a subset of itself, ARA for all A ∈ P(X).
∴R is reflexive.
Let ARB ⇒ A ⊂ B.
This cannot be implied to B ⊂ A.
For instance, if A = {1, 2} and B = {1, 2, 3}, then it cannot be implied that B is related to A.
∴ R is not symmetric.
Further, if ARB and BRC, then A ⊂ B and B ⊂ C.
⇒ A ⊂ C
⇒ ARC
∴ R is transitive.
Hence, R is not an equivalence relation since it is not symmetric.
Question9. Given a non-empty set X, consider the binary operation *: P(X) × P(X) → P(X) given by A * B = A ∩ B & mn For E; A, B in P(X) is the power set of X. Show that X is the identity element for this operation and X is the only invertible element in P(X) with respect to the operation*.
Solution :
Let S be a non-empty set and P(S) be its power set. Let any two subsets A and B of S.

Question10. Find the number of all onto functions from the set {1, 2, 3, … , n) to itself.
Solution :
Onto functions from the set {1, 2, 3, … ,n} to itself is simply a permutation on n symbols 1, 2, …, n.
Thus, the total number of onto maps from {1, 2, …, n} to itself is the same as the total number of permutations on n symbols 1, 2, …, n, which is n!.
11. Let S = {a, b, c} and T = {1, 2, 3}. Find F−1 of the following functions F from S to T, if it exists.
(i) F = {(a, 3), (b, 2), (c, 1)} (ii) F = {(a, 2), (b, 1), (c, 1)}
Solution :
S = {a, b, c}, T = {1, 2, 3}
(i) F: S → T is defined as:
F = {(a, 3), (b, 2), (c, 1)}
⇒ F (a) = 3, F (b) = 2, F(c) = 1
Therefore, F−1: T → S is given by
F−1 = {(3, a), (2, b), (1, c)}.
(ii) F: S → T is defined as:
F = {(a, 2), (b, 1), (c, 1)}
Since F (b) = F (c) = 1, F is not one-one.
Hence, F is not invertible i.e., F−1 does not exist.
Question12. Consider the binary operations*: R ×R → and o: R × R → R defined as a * b = |a – b| and ao b = a, & mn For E; a, b ∈ R. Show that * is commutative but not associative, o is associative but not commutative. Further, show that &mn For E;a, b, c ∈ R, a*(b o c) = (a * b) o (a * c). [If it is so, we say that the operation * distributes over the operation o]. Does o distribute over *? Justify your answer.
answer.
Solution :


Question13. Given a non-empty set X, let *: P(X) × P(X) → P(X) be defined as A * B = (A − B) ∪ (B − A), & mn For E; A, B ∈ P(X). Show that the empty set Φ is the identity for the operation * and all the elements A of P(X) are invertible with A−1 = A. (Hint: (A − Φ) ∪ (Φ − A) = A and (A − A) ∪ (A − A) = A * A = Φ).
Solution :
: It is given that ∗: P(X) × P(X) → P(X) be defined as
A * B = (A – B) ∪ (B – A), A, B ∈ P(X).
Now, let A ϵ P(X). Then, we get,
A * ф = (A – ф) ∪ (ф –A) = A∪ф = A
ф * A = (ф – A) ∪ (A – ф ) = ф∪A = A
A * ф = A = ф * A, A ϵ P(X)
Therefore, ф is the identity element for the given operation *.
Now, an element A ϵ P(X) will be invertible if there exists B ϵ P(X) such that
A * B = ф = B * A. (as ф is an identity element.)
Now, we can see that A * A = (A –A) ∪ (A – A) = ф∪ф = ф AϵP(X).
Therefore, all the elements A of P(X) are invertible with A-1 = A.
Question14. Define binary operation * on the set {0, 1, 2, 3, 4, 5} as
Show that zero is the identity for this operation and each element a ≠ 0 of the set is invertible with 6 – being the inverse of a
Solution :

| * | 0 | 1 | 2 | 3 | 4 | 5 |
| 0 | 0 | 1 | 2 | 3 | 4 | 5 |
| 1 | 1 | 2 | 3 | 4 | 5 | 0 |
| 2 | 2 | 3 | 4 | 5 | 0 | 1 |
| 3 | 3 | 4 | 5 | 0 | 1 | 2 |
| 4 | 4 | 5 | 0 | 1 | 2 | 3 |
| 5 | 5 | 0 | 1 | 2 | 3 | 4 |
Question15. Let A = {–1, 0, 1, 2}, B = {–4, –2, 0, 2} and f; g: A→B be the functions defined by f(x) = x2 − x, x ∈ A and g(x) = 2x – 1/2 – 1. x ∈ A. Are f and g equal? Justify your answer.
(Hint: One may note that two functions f: A → B and g: A → B such that f(a) = g(a) &mnForE;a ∈A,, are called equal functions).
Solution :

Question16. Let A = {1, 2, 3}. Then a number of relations containing (1, 2) and (1, 3) which are reflexive and symmetric but not transitive is:
(A) 1
(B) 2
(C) 3
(D) 4
Solution :
It is clear that 1 is reflexive and symmetric but not transitive.
Therefore, option (A) is correct.
Question17. Let A = {1, 2, 3}. Then a number of equivalence relations containing (1, 2) is:
(A) 1
(B) 2
(C) 3
(D) 4
Solution :
2, Therefore, option (B) is correct.
Question18. Let R → R be the Signum Function defined as an R → R be the Greatest Function given by g(x) = [x] where [x] is the greatest integer less than or equal to x
Then, do fog and gof coincide in (0, 1)?
Solution :

Therefore, option (B) is correct.
Question19. A number of binary operations on the set {a, b} are:
(A) 10
(b) 16
(C) 20
(D) 8
Solution :
A binary operation * on {a, b} is a function from {a, b} × {a, b} → {a, b}
i.e., * is a function from {(a, a), (a, b), (b, a), (b, b)} → {a, b}.
Hence, the total number of binary operations on the set {a, b} is 24 i.e., 16.
The correct answer is B.