NCERT solutions for class 12 maths Chapter 1 Relation and Functions are prepared by the academic team of Nashad. We have prepared NCERT Solutions for all exercises of chapter 1. Given below is a step-by-step solution to all questions given in the NCERT textbook for Chapter 1 Relations and Functions.
NCERT Solutions for Class 12 Maths Exercise 1.4
Solve The Following Questions.
Question1. Determine whether or not each of the definitions given below gives a binary operation. In the event that * is not a binary operation, give justification for this.
(i) On Z+, define * by a * b = a − b
(ii) On Z+, define * by a * b = ab
(iii) On R, define * by a * b = ab2
(iv) On Z+, define * by a * b = |a − b|
(v) On Z+, define * by a * b = a
Solution :
(i) On Z+, * is defined by a * b = a − b.
It is not a binary operation as the image of (1, 2) under * is 1 * 2 = 1 − 2
= −1 ∉ Z+.
(ii) On Z+, * is defined by a * b = ab.
It is seen that for each a, b ∈ Z+, there is a unique element ab in Z+.
This means that * carries each pair (a, b) to a unique element a * b = ab in Z+.
Therefore, * is a binary operation.
(iii) On R, * is defined by a * b = ab2.
It is seen that for each a, b ∈ R, there is a unique element ab2 in R.
This means that * carries each pair (a, b) to a unique element a * b = ab2 in R.
Therefore, * is a binary operation.
(iv) On Z+, * is defined by a * b = |a − b|.
It is seen that for each a, b ∈ Z+, there is a unique element |a − b| in Z+.
This means that * carries each pair (a, b) to a unique element a * b = |a − b| in Z+.
Therefore, * is a binary operation.
(v) On Z+, * is defined by a * b = a.
* carries each pair (a, b) to a unique element a * b = a in Z+.
Therefore, * is a binary operation.
Question2. For each binary operation * defined below, determine whether * is commutative or associative:
(i) On Z, define a * b = a − b
(ii) On Q, define a * b = ab + 1
(iii) On Q, define a * b =ab/2
(iv) On Z+, define a * b = 2ab
(v) On Z+, define a * b = ab
(vi) On R − {−1}, define a.b = a/b+1
Solution :
(i) On Z, * is defined by a * b = a − b.
It can be observed that 1 * 2 = 1 − 2 = 1 and 2 * 1 = 2 − 1 = 1.
∴1 * 2 ≠ 2 * 1; where 1, 2 ∈ Z
Hence, the operation * is not commutative.
Also we have:
(1 * 2) * 3 = (1 − 2) * 3 = −1 * 3 = −1 − 3 = −4
1 * (2 * 3) = 1 * (2 − 3) = 1 * −1 = 1 − (−1) = 2
∴(1 * 2) * 3 ≠ 1 * (2 * 3) ; where 1, 2, 3 ∈ Z
Hence, the operation * is not associative.
(ii) On Q, * is defined by a * b = ab + 1.
It is known that:
ab = ba &mnForE; a, b ∈ Q
⇒ ab + 1 = ba + 1 &mnForE; a, b ∈ Q
⇒ a * b = a * b &mnForE; a, b ∈ Q
Therefore, the operation * is commutative.
It can be observed that:
(1 * 2) * 3 = (1 × 2 + 1) * 3 = 3 * 3 = 3 × 3 + 1 = 10
1 * (2 * 3) = 1 * (2 × 3 + 1) = 1 * 7 = 1 × 7 + 1 = 8
∴(1 * 2) * 3 ≠ 1 * (2 * 3) ; where 1, 2, 3 ∈ Q
Therefore, the operation * is not associative.
(iii) On Q, * is defined by a * b = ab/2
It is known that:
ab = ba &mnForE; a, b ∈ Q
⇒ ab/2 = ba/2 &mn ForE; a, b ∈ Q
⇒ a * b = b * a &mnForE; a, b ∈ Q
Therefore, the operation * is commutative.
For all a, b, c ∈ Q, we have:
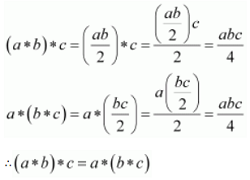
Therefore, the operation * is associative.
(iv) On Z+, * is defined by a * b = 2ab.
It is known that:
ab = ba &mnForE; a, b ∈ Z+
⇒ 2ab = 2ba &mnForE; a, b ∈ Z+
⇒ a * b = b * a &mnForE; a, b ∈ Z+
Therefore, the operation * is commutative.
It can be observed that:
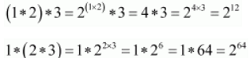
∴(1 * 2) * 3 ≠ 1 * (2 * 3) ; where 1, 2, 3 ∈ Z+
Therefore, the operation * is not associative.
(v) On Z+, * is defined by a * b = ab.
It can be observed that:
1 x2 = 12=1 and 2x 1 =21 = 2
∴ 1 * 2 ≠ 2 * 1 ; where 1, 2 ∈ Z+
Therefore, the operation * is not commutative.
It can also be observed that:
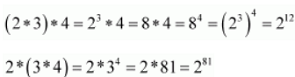
∴(2 * 3) * 4 ≠ 2 * (3 * 4) ; where 2, 3, 4 ∈ Z+
Therefore, the operation * is not associative.
(vi) On R, * − {−1} is defined by a.b = a/b+1
It can be observed that 1 x 2 = 1/2+1 = 1/2 and 2 x 1 = 2/1+1 = 2/2
∴1 * 2 ≠ 2 * 1 ; where 1, 2 ∈ R − {−1}
Therefore, the operation * is not commutative.
It can also be observed that:
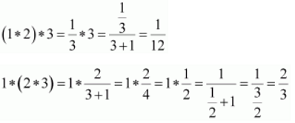
∴ (1 * 2) * 3 ≠ 1 * (2 * 3) ; where 1, 2, 3 ∈ R − {−1}
Therefore, the operation * is not associative.
Question3. Consider the binary operation ∨ on the set {1, 2, 3, 4, 5} defined by a ∨b = min {a, b}. Write the operation table of the operation∨.
Solution :
The binary operation ∨ on the set {1, 2, 3, 4, 5} is defined as a ∨ b = min {a, b} & mn For E; a, b ∈ {1, 2, 3, 4, 5}.
Thus, the operation table for the given operation ∨ can be given as:
| ∨ | 1 | 2 | 3 | 4 | 5 |
| 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 2 | 2 | 2 | 2 |
| 3 | 1 | 2 | 3 | 3 | 3 |
| 4 | 1 | 2 | 3 | 4 | 4 |
| 5 | 1 | 2 | 3 | 4 | 5 |
4. Consider a binary operation * on the set {1, 2, 3, 4, 5} given by the following multiplication table.
(i) Compute (2 * 3) * 4 and 2 * (3 * 4)
(ii) Is * commutative?
(iii) Compute (2 * 3) * (4 * 5).
(Hint: use the following table)
| * | 1 | 2 | 3 | 4 | 5 |
| 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 2 | 1 | 2 | 1 |
| 3 | 1 | 1 | 3 | 1 | 1 |
| 4 | 1 | 2 | 1 | 4 | 1 |
| 5 | 1 | 1 | 1 | 1 | 5 |
Solution :
(i) (2 * 3) * 4 = 1 * 4 = 1
2 * (3 * 4) = 2 * 1 = 1
(ii) For every a, b ∈{1, 2, 3, 4, 5}, we have a * b = b * a. Therefore, the operation * is commutative.
(iii) (2 * 3) = 1 and (4 * 5) = 1
∴(2 * 3) * (4 * 5) = 1 * 1 = 1
Question5. Let*′ be the binary operation on the set {1, 2, 3, 4, 5} defined by a *′ b = H.C.F. of a and b. Is the operation *′ same as the operation * defined in Exercise 4 above? Justify your answer.
Solution :
The binary operation *′ on the set {1, 2, 3 4, 5} is defined as a *′ b = H.C.F of a and b.
The operation table for operation *′ can be given as:
| *′ | 1 | 2 | 3 | 4 | 5 |
| 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 2 | 1 | 2 | 1 |
| 3 | 1 | 1 | 3 | 1 | 1 |
| 4 | 1 | 2 | 1 | 4 | 1 |
| 5 | 1 | 1 | 1 | 1 | 5 |
We observe that the operation tables for the operations * and *′ are the same.
Thus, the operation *′ is the same as the operation*.
Question6. Let * be the binary operation on N given by a * b = L.C.M. of a and b. Find
(i) 5 * 7, 20 * 16 (ii) Is * commutative?
(iii) Is * associative? (iv) Find the identity of * in N
(v) Which elements of N are invertible for the operation *?
Solution :
The binary operation * on N is defined as a * b = L.C.M. of a and b.
(i) 5 * 7 = L.C.M. of 5 and 7 = 35
20 * 16 = L.C.M of 20 and 16 = 80
(ii) It is known that:
L.C.M of a and b = L.C.M of b and a &mnForE; a, b ∈ N.
∴a * b = b * a
Thus, the operation * is commutative.
(iii) For a, b, c ∈ N, we have:
(a * b) * c = (L.C.M of a and b) * c = LCM of a, b, and c
a * (b * c) = a * (LCM of b and c) = L.C.M of a, b, and c
∴(a * b) * c = a * (b * c)
Thus, the operation * is associative.
(iv) It is known that:
L.C.M. of a and 1 = a = L.C.M. 1 and a &mnForE; a ∈ N
⇒ a * 1 = a = 1 * a &mnForE; a ∈ N
Thus, 1 is the identity of * in N.
(v) An element a in N is invertible with respect to the operation * if there exists an element b in N, such that a * b = e = b * a.
Here, e = 1
This means that:
L.C.M of a and b = 1 = L.C.M of b and a
This case is possible only when a and b are equal to 1.
Thus, 1 is the only invertible element of N with respect to the operation *.
Question7. Is * defined on the set {1, 2, 3, 4, 5} by a * b = L.C.M. of a and b a binary operation? Justify your answer.
Solution :
The operation * on the set A = {1, 2, 3, 4, 5} is defined as
a * b = L.C.M. of a and b.
Then, the operation table for the given operation * can be given as:
| * | 1 | 2 | 3 | 4 | 5 |
| 1 | 1 | 2 | 3 | 4 | 5 |
| 2 | 2 | 2 | 6 | 4 | 10 |
| 3 | 3 | 6 | 3 | 12 | 15 |
| 4 | 4 | 4 | 12 | 4 | 20 |
| 5 | 5 | 10 | 15 | 20 | 5 |
It can be observed from the obtained table that:
3 * 2 = 2 * 3 = 6 ∉ A, 5 * 2 = 2 * 5 = 10 ∉ A, 3 * 4 = 4 * 3 = 12 ∉ A
3 * 5 = 5 * 3 = 15 ∉ A, 4 * 5 = 5 * 4 = 20 ∉ A
Hence, the given operation * is not a binary operation.
Question8. Let * be the binary operation on N defined by a * b = H.C.F. of a and b. Is * commutative? Is * associative? Does there exist an identity for this binary operation on N?
Solution :
The binary operation * on N is defined as:
a * b = H.C.F. of a and b
It is known that:
H.C.F. of a and b = H.C.F. of b and a &mnForE; a, b ∈ N.
∴a * b = b * a
Thus, the operation * is commutative.
For a, b, c ∈ N, we have:
(a * b)* c = (H.C.F. of a and b) * c = H.C.F. of a, b, and c
a *(b * c)= a *(H.C.F. of b and c) = H.C.F. of a, b, and c
∴(a * b) * c = a * (b * c)
Thus, the operation * is associative.
Now, an element e ∈ N will be the identity for the operation * if a * e = a = e* a ∈ a ∈ N.
But this relation is not true for any a ∈ N.
Thus, the operation * does not have any identity in N.
Question9. Let * be a binary operation on the set Q of rational numbers as follows:
(i) a * b = a − b
(ii) a * b = a2 + b2
(iii) a * b = a + ab
(iv) a * b = (a − b)2
(v) a * b = ab/4 (vi) a * b = ab2
Find which of the binary operations are commutative and which are associative.
Ans.




10. Find which of the operations given above has an identity.
Solution :
Let the identity be I.

Question 11. Let A = N × N and * be the binary operation on A defined by
(a, b) * (c, d) = (a + c, b + d)
Show that * is commutative and associative. Find the identity element for * on A, if any.
Solution :
A = N × N
* is a binary operation on A and is defined by:
(a, b) * (c, d) = (a + c, b + d)
Let (a, b), (c, d) ∈ A
Then, a, b, c, d ∈ N
We have:
(a, b) * (c, d) = (a + c, b + d)
(c, d) * (a, b) = (c + a, d + b) = (a + c, b + d)
[Addition is commutative in the set of natural numbers]
∴(a, b) * (c, d) = (c, d) * (a, b)
Therefore, the operation * is commutative.
Now, let (a, b), (c, d), (e, f) ∈A
Then, a, b, c, d, e, f ∈ N
We have:

Question12. State whether the following statements are true or false. Justify.
(i) For an arbitrary binary operation * on a set N, a * a = a ∀ a * N.
(ii) If * is a commutative binary operation on N, then a * (b * c) = (c * b) * a
Solution :
(i) Define an operation * on N as:
a * b = a + b a, b ∈ N
Then, in particular, for b = a = 3, we have:
3 * 3 = 3 + 3 = 6 ≠ 3
Therefore, statement (i) is false.
(ii) R.H.S. = (c * b) * a
= (b * c) * a [* is commutative]
= a * (b * c) [Again, as * is commutative]
= L.H.S.
∴ a * (b * c) = (c * b) * a
Therefore, statement (ii) is true.
Question13. Consider a binary operation * on N defined as a * b = a3 + b3. Choose the correct answer.
(A) Is * both associative and commutative?
(B) Is * commutative but not associative?
(C) Is * associative but not commutative?
(D) Is * neither commutative nor associative?
Solution :
On N, the operation * is defined as a * b = a3 + b3.
For, a, b, ∈ N, we have:
a * b = a3 + b3 = b3 + a3 = b * a [Addition is commutative in N]
Therefore, the operation * is commutative.
It can be observed that:
(1*2)*3 = (13+23)*3 = 9 * 3 = 93 + 33 = 729 + 27 = 756
Also, 1*(2*3) = 1*(23 +33) = 1*(8 +27) = 1 × 35
= 13 +353 = 1 +(35)3 = 1 + 42875 = 42876.
∴(1 * 2) * 3 ≠ 1 * (2 * 3) ; where 1, 2, 3 ∈ N
Therefore, the operation * is not associative.
Hence, the operation * is commutative, but not associative. Thus, the correct answer is B.