Class 12 Maths

NCERT SOLUTIONS FOR CLASS 12 MATHS CHAPTER 1-RELATIONS AND FUNCTIONS EXERCISE 1.2

NCERT solutions for class 12 maths Chapter 1 Relation and Functions is prepared by the academic team of Nashad.in, We have prepared  NCERT Solutions for all exercises of chapter 1. Given below is a step-by-step solution to all questions given in the NCERT textbook for Chapter 1 Relations and Functions.

Question1. Show that the function f: R* → R* defined by f(x) = 1/x is one-one and onto, where: R* is the set of all non-zero real numbers. Is the result true, if the domain: R* is replaced by N with the co-domain being the same as R_*?

Solution :

Hence, function g is one-one but not onto.

Question2. Check the injectivity and surjectivity of the following functions:

(i) f: N → N given by f(x) = x²

(ii) f: Z → Z given by f(x) = x² 

(iii) f: R → R given by f(x) = x²

(iv) f: N → N given by f(x) = x³

(v) f: Z → Z given by f(x) = x³

Solution :
(i) f: N → N is given by,

f(x) = x²

It is seen that for x, y ∈N, f(x) = f(y)

⇒ x² = y² ⇒ x = y.

∴f is injective. 

Now, 2 ∈ N. But, there does not exist any x in N such that f(x) = x² = 2.

∴ f is not surjective.

Hence, function f is injective but not surjective.

(ii) f: Z → Z is given by,

f(x) = x²

It is seen that f(−1) = f(1) = 1, but −1 ≠ 1.

∴ f is not injective.

Now,−2 ∈ Z. But, there does not exist any element x ∈Z such that f(x) = x² = −2.

∴ f is not surjective.

Hence, function f is neither injective nor surjective.

(iii) f: R → R is given by,

f(x) = x²

It is seen that f(−1) = f(1) = 1, but −1 ≠ 1.

∴ f is not injective.

Now,−2 ∈ R. But, there does not exist any element x ∈ R such that f(x) = x² = −2.

∴ f is not surjective.

Hence, function f is neither injective nor surjective.

(iv) f: N → N given by,

f(x) = x³

It is seen that for x, y ∈N, f(x) = f(y)

⇒ x³ = y³ ⇒ x = y.

∴f is injective.

Now, 2 ∈ N. But, there does not exist any element x in domain N such that f(x) = x³ = 2.

∴ f is not surjective

Hence, function f is injective but not surjective.

(v) f: Z → Z is given by,

f(x) = x³

It is seen that for x, y ∈ Z, f(x) = f(y)

⇒ x³ = y³ ⇒ x = y.

∴ f is injective. 

Now, 2 ∈ Z. But, there does not exist any element x in domain Z such that f(x) = x³ = 2.

∴ f is not surjective.

Hence, function f is injective but not surjective.

Question3. Prove that the Greatest Integer Function f: R → R given by f(x) = [x], is neither one-one nor onto, where [x] denotes the greatest integer less than or equal to x.

Solution :
f: R → R is given by,

f(x) = [x]

It is seen that f(1.2) = [1.2] = 1, f(1.9) = [1.9] = 1.

∴ f(1.2) = f(1.9), but 1.2 ≠ 1.9.

∴ f is not one-one.

Now, consider 0.7 ∈ R.

It is known that f(x) = [x] is always an integer. Thus, there does not exist any element x ∈ R such that f(x) = 0.7.

∴ f is not onto.

Hence, the greatest integer function is neither one-one nor onto.

Question4. Show that the Modulus Function f : R → R, given by f(x) = |x| is neither one-one nor onto, where is |x| if  x is positive or 0 and |-x| is -x  if  x is negative.

Solution :

Question5. Show that the Signum Function f: R → R, given by

 is neither one-one nor onto.

Solution :

f: R → R

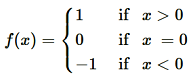
It is seen that f(1) = f(2) = 1, but 1 ≠ 2.

∴ f  is not one-one.

Now, as f(x) ) takes only 3 values (1, 0, or −1) for the element −2 in co-domain R , there does not exist any x  in domain R  such that

f(x) = −2.

∴ f  is not onto.

Hence, the signum function is neither one-one nor onto.

Question6. Let A = {1, 2, 3}, B = {4, 5, 6, 7} and let f = {(1, 4), (2, 5), (3, 6)} be a function from A to B. Show that f is one-one.

Solution :
It is given that A = {1, 2, 3}, B = {4, 5, 6, 7}.

f: A → B is defined as f = {(1, 4), (2, 5), (3, 6)}.

∴ f (1) = 4, f (2) = 5, f (3) = 6

It is seen that the images of distinct elements of A under f are distinct.

Hence, function f is one-one.

Question7. In each of the following cases, state whether the function is one-one, onto, or bijective. Justify your answer.

(i) f: R → R defined by f(x) = 3 − 4x

(ii) f: R → R defined by f(x) = 1 + x²

Solution :
 

Question8. Let A and B be sets. Show that f: A × B → B × A such that (a, b) = (b, a) is a bijective function.

Solution :
 

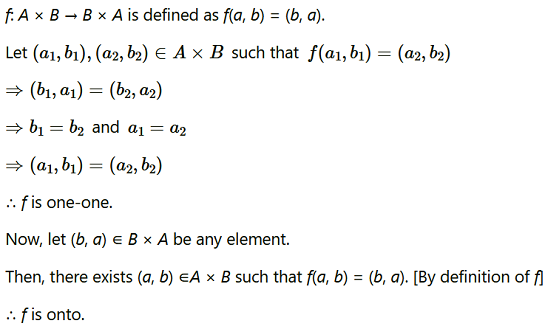
Question9. Let N → N be  defined by f(n)  for all

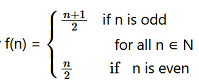
State whether the function f is bijective. Justify your answer.

Solution :

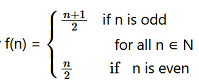
Question10. Let A = R – {3} and B = R – {1}. Consider the function f : A → B defined by f(x)  = (x-2/x-3) Is f one-one and onto? Justify your answer.

Solution :
A = R – {3} and B = R – {1}

f : A → B defined by f(x)  = (x-2/x-3)

Let x, y ∈ A such that f(x) =  f(y)

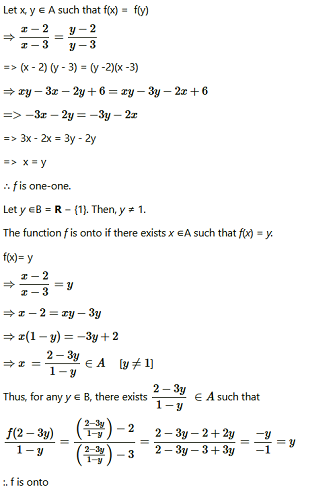
Hence, function f  is one-one and onto.

Question11. Let f: R → R be defined as f(x) = x⁴. Choose the correct answer.

(A) f is one-one onto

(B) f is many-one onto

(C) f is one-one but not onto

(D) f is neither one-one nor onto

Solution :

f: R→ R is defined as f(x) = x⁴.

Let ,x, y ∈ R  such that f(x) = f(y).

⇒ x⁴ = y⁴

⇒ x = ±y

∴f(x₁) = f (_x2)  does not imply that x₁ = x₂

For instance,

f(1) = f(-1) = 1

∴ f  is not one-one.

Consider an element 2 in co-domain R . It is clear that there does not exist any x  in domain  R  such that f(x) = 2.

∴ f  is not onto.

Hence, function f  is neither one-one nor onto.

The correct answer is D.

Question12. Let f: R → R be defined as f(x) = 3x. Choose the correct answer.

(A) f is one-one onto

(B) f is many-one onto

(C) f is one-one but not onto

(D) f is neither one-one nor onto

Solution : f: R → R be defined as f(x) = 3x.

Let ,x, y ∈ R  such that f(x) = f(y).

⇒ 3x = 3y

⇒ x = y

∴ f is one – one

Also, for any real number (y)  in co-domain R, there exists y/3 in R  such that f(y/3) = 3(y/3) = y

∴ f is onto.

Hence, function f  is one-one and onto.

The correct answer is A.